Inertial Response
Frequency Responses
The rotating masses of the generators and motors on the system store kinetic energy. The amount of this stored energy is proportional to the system inertia M, and, therefore, the larger the M the larger the kinetic energy stored. Following a disturbance that results in a generation loss, the frequency starts to decay and this results in the release of the stored kinetic energy in the form of power which is referred to as Inertial Response. This response, consistent with D’Alambert’s principle, is given by the following equation :
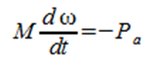
(1)
Where:
M = System inertia (angular momentum) in J-s/rad
ω = System angular speed in rad/s
Pa = Accelerating power which, at ω0, equals the amount of generation lost which is the same as the excess load.
The expression on the left hand side of equation (1) represents the Inertial Response power which, therefore, is proportional to M and the frequency rate of change. Accordingly, for a given value of Pa, the rate of change is directly proportional to Pa and inversely proportional to M. Thus, for a given generation loss, M determines how fast frequency can change following the loss.The higher the M the slower the rate of change. Therefore, higher values of M translate into more stable operation and, therefore, play a critical role in ensuring a stable transition from predisturbance to post disturbance conditions. Once the system has remained stable, the higher inertia lowers the frequency decay rate and thus results in more time available for the implementation of remedial actions such as governor response. Equation (1) also illustrates the fact that the the excess load keeps being supplied by the Inertial Response until a new equilibrium point is reached at a lower frequency.
It is important to note that the Inertial Response contributed by M is not the same as Equipment Frequency Response (EFR) or Governor Frequency Response (GFR). The fundamental difference is as follows. The EFR and GFR together determine the value at which the frequency decay is arrested and impact the time that it takes to get there; M, however, only impacts the time that it takes to get to the arrested frequency value. Once the frequency is arrested, the impact of M vanishes. It is of interest to notice that the same factors that slow down and arrest the frequency decay, also slow down the frequency recovery.
