Frequency Deviation Equation
Frequency Responses
Page edited on December 3, 2018
1.0 Introduction
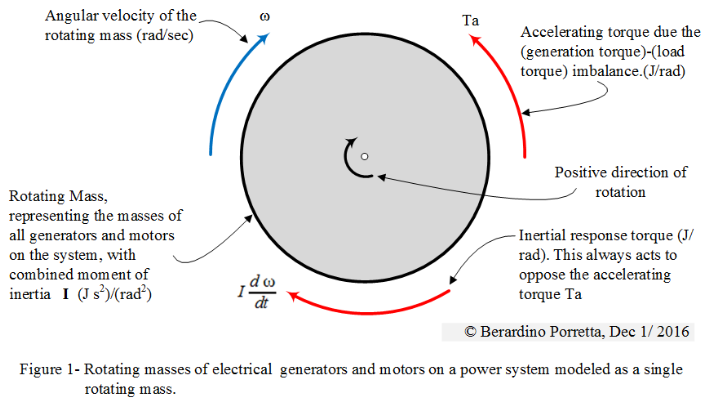
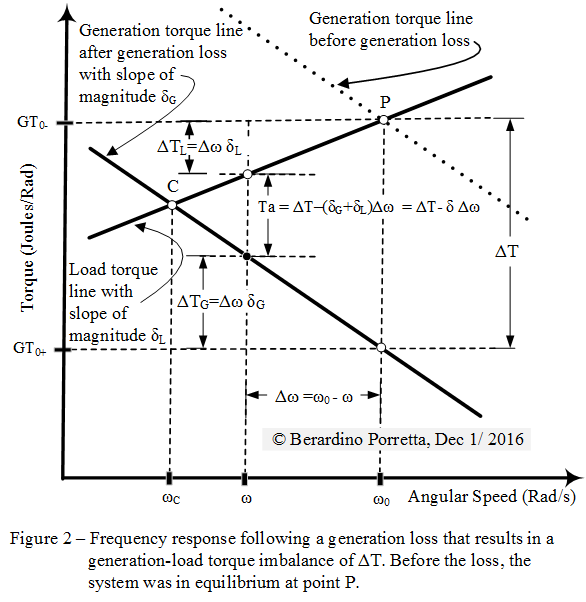
Our interconnections are very complex systems consisting of several generators, motor loads and other loads, transformers and other equipment. The analysis of the transient and dynamic behaviour of these systems for planning or operating purposes is very complex and requires careful modeling of the individual generators, loads and other equipment. It is noteworthy that the application programs used to analyze theses transient and dynamic behaviour do not calculate a system frequency. Rather, they calculate the frequency of each of the rotating machines oscillating against each other. If the system frequency is needed, say as viewed by an underfrequency protection relay, such frequency has to be estimated from the frequencies of the individual machines modeled. One method that has been used is to calculated the system frequency as the weighted average of the frequencies of the individual machines using the respective machines inertia constants as the weighting factor. When the frequency excursion following significant generation loss incident is measureds, the frequency meter is in effect viewing the system as if it were a single generator with a mass equivalent to that of all the rotating machines on the system, and the meter is "calculating" some weighted average of the frequencies of the individual synchronous machines rotating on the system . An equation that models the frequency deviation of these systems as viewed by a frequency meter can be very useful because the results would be reasonably accurate while the data and computational requirements would be very modest. This modesty would permit the quick evaluation of several scenarios for analyses such as:
1. Extracting from the measured frequency excursion curves, following significant loss of generation events, parameters such as: system inertia; system frequency response from governors; system frequency response from system self regulation; and governor response withdrawal.
2. Calculating the impact of solar and wind generation on system inertia and frequency response.
3. Calculating the percentage of system inertia contributed by motor loads.
4. Tuning the settings of load shedding and of generators underfrequency protection schemes.
5. Assessing the amount of synchronous generation required on line to guarantee sufficient frequency and inertial response at operating time for different
solar and wind penetration scenarios.
This page derives such a frequency deviation equation for the system viewed as a single equivalent machine.